Sólo me quedan las estrellas. DISEÑOS DE DOS GRUPOS. MUESTRAS RELACIONADAS
Suzanne Vega - Luka
"Luka"
My name is Luka
I live on the second floor
I live upstairs from you
Yes I think you've seen me before
If you hear something late at night
Some kind of trouble. some kind of fight
Just don't ask me what it was
Just don't ask me what it was
Just don't ask me what it was
I think it's because I'm clumsy
I try not to talk too loud
Maybe it's because I'm crazy
I try not to act too proud
They only hit until you cry
After that you don't ask why
You just don't argue anymore
You just don't argue anymore
You just don't argue anymore
Yes I think I'm okay
I walked into the door again
Well, if you ask that's what I'll say
And it's not your business anyway
I guess I'd like to be alone
With nothing broken, nothing thrown
Just don't ask me how I am
My name is Luka
I live on the second floor
I live upstairs from you
Yes I think you've seen me before
If you hear something late at night
Some kind of trouble, some kind of fight
Just don't ask me what it was
Just don't ask me what it was
Just don't ask me what it was
And they only hit until you cry
After that, you don't ask why
You just don't argue anymore
You just don't argue anymore
You just don't argue anymore
I live on the second floor
I live upstairs from you
Yes I think you've seen me before
If you hear something late at night
Some kind of trouble. some kind of fight
Just don't ask me what it was
Just don't ask me what it was
Just don't ask me what it was
I think it's because I'm clumsy
I try not to talk too loud
Maybe it's because I'm crazy
I try not to act too proud
They only hit until you cry
After that you don't ask why
You just don't argue anymore
You just don't argue anymore
You just don't argue anymore
Yes I think I'm okay
I walked into the door again
Well, if you ask that's what I'll say
And it's not your business anyway
I guess I'd like to be alone
With nothing broken, nothing thrown
Just don't ask me how I am
My name is Luka
I live on the second floor
I live upstairs from you
Yes I think you've seen me before
If you hear something late at night
Some kind of trouble, some kind of fight
Just don't ask me what it was
Just don't ask me what it was
Just don't ask me what it was
And they only hit until you cry
After that, you don't ask why
You just don't argue anymore
You just don't argue anymore
You just don't argue anymore
Sólo me quedan las estrellas
El cielo majorero que se abre ante mi todas las noches, me evoca nostalgias infantiles que se diluyen entre las lecturas no tan infantes a las que siempre me he expuesto. Mirar hacia arriba y percibir que una legión estelar cae encima de tus hombros sin tocarte es una de las experiencias que no puedo transmitir ni describir. Sólo capto una confianza invisible que silenciosamente indica seguir adelante. Simplemente eso, seguir adelante.
Algo ensombrecida me hallo. Me encuentro ante una tesitura constante en mi vida. Los asuntos eclesiásticos andan revueltos por los "presuntos" abusos sexuales perpetrados por sacerdotes a monaguillos, y el jefe de todos los sacerdotes dice que tolerancia cero con eso.
Bien, hasta ahí normalidad en el telediario, hace pocos días nos dijeron que habían detenido al violador de Ciudad Lineal, y de vez en cuando nos dicen que han pillado a algún violador que otro. Todo muy normal en los noticieros. Salen psicólogos, en los diferentes debates, dando perfiles de los violadores, psicólogos que describen el perfil de los abusados, abogados que dicen como van las cosas por los libros teóricos del Derecho. Todo muy normal.
Pero claro no puedo dejar de ser inquieta, es superior a mi, y me meto en terrenos en los que (como siempre) la perjudicada soy yo, y nadie más que yo. Y no escarmiento. No aprendo.
Mirando por el twitter vi un tweet de una revista que sigo que expuso con "ironía" una noticia referida a curas y niños y abusos sexuales. Mandé un correo a la editorial y me contestaron enseguida.
Ésta fue mi misiva on line:
Y esto lo que muy amablemente contestaron enseguida:
Pues como siempre me invadió la indefensión, y el sentirme "tonta", inútil, analfabeta, ignorante, y todas las demás lindezas que me entran en temas de estos, porque está claro por la contestación que mi sensibilidad es muy equivocada ya que me ofenden el chiste y no el acto..... y se quedan tan estupendos con sus carreras universitarias terminadas, con sus nóminas llenas, y sus cuentas bancarias al día, y claro la que está equivocada soy yo porque no estoy criticando el acto y critico la ironía con la que "estos defensores del alma humana" han criticado el acto. Vamos que los héroes son los creadores del chiste y por supuesto yo soy la que tengo que orientar mejor mis asuntos cognitivos ya que no ataco el acto y si los chistes.
Me quedé completamente desarmada cognitivamente, y como siempre me entró la llantina, por eso indiqué antes que siempre la perjudicada soy yo. Pero bueno, ya con 48 años y con un currículum vital de criar tres hijos, pues como que soy insignificante en este mar de intereses geopolíticos-económicos.
En fin que si, que mi pobre cerebro no da para más en este devenir de los abusos sexuales. Se utiliza un arma de guerra contra las mujeres y los niños, se ironiza con ello, se compran mercaderías, se producen intercambios de fotografías en situación de indefensión total, siendo las revistas con la premisa de "ganar dinero" y no con la premisa de denunciar los actos, las que usando una lingüística ambigua y engatusadora de los violadores y pederastas, aplauden unas consignas prehistóricas y cavernarias, vamos completamente de cerebros reptilianos sin evolucionar siquiera a cerebro mamífero. Pero claro la "tonta soy yo" que no comprendo lo que es una ironía, o tengo una sensibilidad muy sensible y no sirve mi opinión. Mientras tanto y en base a los "hechos y actos" ocurridos, realizan una serie de "bromas, chistes, ironías, burla - causticidad - humor - dardo - donaire - guasa - lindeza - mordacidad -reticencia - sarcasmo - sátira - socarronería y demás sinónimos que yo como ignorante, analfabeta que soy no acierto a comprender.
Pero claro algo que se está utilizando en el planeta Tierra en todos los continentes y que desde la guerra de los Balcanes en los 90 le pusieron nombre y apellido a una atrocidad que cometen muchos seres humanos como arma de guerra. Si, la violación a mujeres y a niños se considera un arma de guerra y que en los países sin conflicto bélico se utiliza como medio de control familiar, de negocio y religioso. Pero claro yo no puedo tener ese tipo de opiniones pues no tengo ni idea de lo que es una ironía ni una broma. Ni tampoco puedo opinar porque no tengo un papelito oficial que diga que soy abogada o psicóloga o policía, o juez, o cualquier honrosa carrera que da derecho existencial a estar por encima del bien y del mal. Simplemente soy una mujer que fue abusada por un familiar durante años y que nadie creyó.
Y desde mi atalaya majorera, con el faro de la Entallada al este, vislumbro un continente que su grandeza y su majestuosidad geográfica no acalla el deshumanismo que sus gentes viven. Hacen falta una legión de ginecólogos y ginecólogas para intentar sanar los aparatos reproductores de millones de mujeres y niños que han sido brutalmente devastados. Sin importarles las consecuencias físicas y psicológicas posteriores, invaden unos cuerpos infantiles que con total impunidad y bajo el nombre de algún dios, de algún comandante o de algún mandamás de turno, van normalizando situaciones grotescas y horrorosas y lo que es peor haciendo adeptos, obligando a los más pequeños a que actúen de esa forma ayudados por sustancias alucinógenas o no. Pero no tengo porque opinar ya que está claro que los asuntos cognitivos no los tengo claros. En un trabajo que tuve, estábamos en la acera de una calle fumando un cigarro y pasó por allí una chica muy linda ella con una minifalda y unos tacones, algún "gracioso, irónico, sarcástico....etc." dijo: "si es que van como putas con esas minifaldas" y otro empezó a reírse, yo dentro de mi ignorancia y mi sentido cognitivo equivocado solté "te gustaría que dijeran eso de tu hija".... y se acabaron las risas..... Claro me dijeron que eso eran bromas y que no me lo tomara así...... Siempre es lo mismo "Mati te lo tomas a la tremenda y tienes que reírte más.....".
http://www.bolyabaenga.org/index.php?option=com_content&view=article&id=99:imirad-a-africa&catid=39:journaliste&Itemid=60
http://www.savethechildren.es/docs/Ficheros/565/SC_Violencia_Sexual_contra_losninosylasninas.pdf
Pues como no viviré un cambio de situación, y seguirán diciendo que soy una exagerada por no reírme de las violaciones y abusos sexuales infantiles, ni de reírme del poder que ejercen los psicópatas de turno, sean curas, chamanes, militares, políticos, familiares o quien sea...... Si que diré que el arma de guerra más antigua que se utiliza es la violación sexual y que en torno a ello hay un negocio mucho más lucrativo que el negocio del petróleo. Pero una simple ama de casa no tiene opinión y menos si fue violada...... ya que su status cognitivo no está en condiciones de tantas deliberaciones ni consideraciones pues ello está destinado a mentes superiores.
Para finalizar esta catarsis un libro y un fragmento del dicho libro.
Y el cachito de fragmento:
Y eso es lo que les pasa a estos niños y mujeres que fueron violadas, que cuando se sienten seguros y seguras es cuando lo cuentan, pasen los años que pasen, hasta que no encuentran seguridad en sus "espíritus", no lo cuentan, mientras tanto habrá silencio y se aferrarán a la nada y en sus momentos de lucidez intentan componer un puzle personal que algún descastado les robó por simple curiosidad o por un impulso mesolímbico incontrolable que la sociedad se empeña en tapar y encubrir como algo consustancial al humano. A eso muchos lo llaman la complejidad de la naturaleza humana. Y yo digo que no se merecen la categorización de Homo sapiens sapiens.
Y yo por mi parte seguiré indicando que las ironías sexuales referentes a niños y niñas no son ni ironías, ni bromas, y que lo que están haciendo con esas bromas, ironías que mi cerebro deteriorado e ignorante no llega, es naturalizar un acto aberrante que va en contra de todo lo que lleve el adjetivo/sustantivo Humano. Pero en un país como el nuestro, que se precia de ir a hacer turismo sexual a todos los países que puede, y que algunos no se han cortado en pregonarlo por televisiones y programas radiofónicos, queda mucho trabajo por hacer en esta materia tan lucrativa para algunas mentes horrorosamente aberrantes.
http://www.acta.es/medios/articulos/ciencias_y_tecnologia/062033.pdf
ANÁLISIS DE DATOS PARA DISEÑOS DE DOS GRUPOS. MUESTRAS RELACIONADAS
Las muestras relacionadas
tienen una ventaja sobre las independientes que consiste en que nos ayudan a
reducir la varianza de error, de manera que cuanto mayor sea la relación entre
ambas muestras, menor será la varianza de la distribución muestral de las
diferencias, obteniendo por lo tanto un estadístico de contraste mayor.
Contraste de
hipótesis sobre dos medias en muestras relacionadas.
Aunque contamos con dos
medias como en el tema anterior, la distribución muestral es diferente, por lo
que comenzaremos este apartado con un breve ejemplo, cuyo fin es exclusivamente
didáctico y que nos servirá para comprender cómo se compone la distribución muestral
de las diferencias.
Distribución muestral para dos medias relacionadas
Supongamos que tenemos una
población compuesta por 4 sujetos a los que medimos la variable dependiente
antes y después de una terapia.
La población sobre la que
vamos a trabajar está formada por las diferencias entre las puntuaciones
“antes” y “después”, o sea, por los valores, una vez ordenados:
Sobre la
población de diferencias, tomamos todas las muestras de un determinado tamaño y
las medias de todas ellas formarán la distribución muestral de las diferencias.
Por ejemplo, para muestras de tamaño n=2, los resultados de todas las muestras
con reposición pueden verse en la Tabla
Por lo que la distribución
muestral de las diferencias está formada por los valores:
- {-2; -0’5; -0’5; 0; 0; 1; 1’5; 1’5; 1’5; 1’5; 2; 3; 3; 3’5; 3’5; 5}
La media y varianza
de la distribución muestral podemos calcularla:
- con los datos de la Tabla
- a través de los parámetros poblacionales
Podemos
apreciar cómo el contraste de hipótesis sobre dos medias relacionadas es muy parecido
al de una sola media.
- Aunque ahora partimos de dos muestras, al estar estas relacionadas, finalmente tenemos una sola variable (las diferencias entre cada par de puntuaciones).
Para
apreciar más claramente esta similitud, vamos a comparar el estadístico de
contraste en ambos casos cuando la varianza poblacional es conocida
Conocida la varianza poblacional de las diferencias.
Ejemplo 4.1. Un psicólogo escolar está interesado en estudiar si la presión
de los padres para el rendimiento escolar es igual en chicos y en chicas.
Toma una
muestra aleatoria de 36 parejas de hermanos (chico y chica), y
mediante un test que proporciona medidas en una escala de intervalo mide la
variable “presión para el rendimiento escolar” en todos los individuos.
- La media para los chicos (Grupo 1) fue igual a 21 y para el grupo de chicas fue igual a 19.
- Suponemos que conocemos la varianza poblacional de las diferencias y que es igual a 64.
A un nivel de
confianza del 99%.
Condiciones y supuestos.
Las muestras de chicos y chicas son relacionadas dado que están compuestas
por parejas de hermanos.
- Conocemos la varianza de las diferencias en la población
- La variable dependiente está medida a un nivel de intervalo
- No sabemos si la población de diferencias se distribuye normalmente, pero la muestra supera las 30 observaciones.
En general, los supuestos
son:
- - Variable dependiente con un nivel de medida de intervalo o razón.
- - Población de diferencias normalmente distribuida o n ≥ 30.
- - Varianza poblacional de las diferencias conocida.
Elección del
estadístico de contrate y su distribución muestral.
El estadístico de contraste
se distribuye normalmente, según la expresión:
Mediante la tabla de curva
normal del apéndice deducimos que:
- la probabilidad de encontrar valores superiores a una puntuación típica de 1’5 es igual a: 0’0668.
Al ser el contraste bilateral,
el nivel crítico p es:
Establecer la
regla de decisión en función del nivel de confianza.
Al nivel de confianza del 99%, los valores
críticos que delimitan la zona en la que mantenemos
Conclusión.
Al nivel de confianza del
99% no existen diferencias significativas entre las medias de chicos y chicas,
puesto que el estadístico de contraste se encuentra comprendido en el intervalo
que definen los valores críticos, por lo que mantenemos la hipótesis nula.
Interpretar el resultado en función del contexto de la investigación.
Interpretar el resultado en función del contexto de la investigación.
Según los datos que manejamos,
no existen diferencias en cuanto a la presión para el rendimiento escolar entre
chicos y chicas.
Intervalo de confianza.
Que con nuestros datos vale:
Observamos que el intervalo
de confianza contiene al cero que es lo que postula la hipótesis nula.
Desconocida la varianza poblacional de las diferencias.
Lo más habitual en un caso
práctico es que desconozcamos la varianza de la población, siendo el proceso
muy parecido al que acabamos de ver.
- Simplemente tenemos que sustituir la varianza poblacional de las diferencias
- por su estimador, que es la cuasivarianza de las diferencias en la muestra.
El estadístico de contraste en este caso se distribuye según t de Student con n - 1 grados de libertad.
Ejemplo 4.2. Un psicólogo que trabaja en una empresa imparte un curso sobre asertividad.
Al finalizar el curso el psicólogo aplica de nuevo el test de asertividad a los asistentes.
Las puntuaciones antes y después del curso fueron las siguientes
Hipótesis
Elección del estadístico de contraste y su distribución muestral.
La representación de los datos queda:
Ejemplo 4.2. Un psicólogo que trabaja en una empresa imparte un curso sobre asertividad.
- El objetivo del curso consiste en fomentar esta habilidad en los directivos que forman parte de su departamento.
Al finalizar el curso el psicólogo aplica de nuevo el test de asertividad a los asistentes.
Las puntuaciones antes y después del curso fueron las siguientes
Con un nivel de confianza
del 95%. Suponiendo que en la población la distribución de las diferencias es
normal,
- ¿Podemos decir que el curso realizado por el psicólogo ha incrementado la asertividad de los directivos?
Antes de realizar el
contraste de hipótesis vamos a calcular las diferencias y los cuadrados de las
mismas entre las condiciones “Antes” y “Después” para cada par de sujetos.
Estos
cálculos son necesarios para calcular la media y la cuasivarianza insesgada.
La media y la varianza insesgada de las puntuaciones diferencia valen:
Condiciones y
supuestos.
Según el enunciado del
problema, la variable dependiente está medida a un nivel de intervalo.
Hemos de
suponer que la población de las diferencias sigue una distribución normal
porque la muestra es pequeña y no conocemos su varianza. En general se tendrá
que cumplir:
- Variable dependiente con un nivel de medida de intervalo o razón.
- Población de diferencias que se distribuye normalmente, o bien n ≥ 30.
- Varianza poblacional de las diferencias desconocida.
Hipótesis
|
|
Elección del estadístico de contraste y su distribución muestral.
El
estadístico de contraste se distribuye según la t de Student con n-1 grados de
libertad, y lo calculamos según la expresión:
Para averiguar el nivel crítico de forma aproximada, buscamos en la tabla t de
Student del apéndice entre que valores se encuentra el estadístico de contraste,
en este caso para 9 grados de libertad observamos:
·
Por lo que el nivel crítico p se encontrará entre los valores:
Establecer la regla de
decisión en función del nivel de confianza.
Los grados de libertad del ejemplo son:
Acudiendo a la tabla t de Student, el valor crítico que delimita cuando mantenemos o
rechazamos la hipótesis nula, a un nivel de confianza del 95%, es - 1’833.
La representación de los datos queda:
Conclusión.
A un nivel de confianza del 95%:
- rechazamos la hipótesis nula puesto que el estadístico de contraste es más extremo que el valor crítico (máxima diferencia que cabe esperar por simple azar).
Por lo que concluimos que:
- la media en asertividad de los directivos es inferior antes que después del curso.
En cualquier caso, los datos obtenidos
superan con creces el nivel de confianza que de antemano había fijado el
psicólogo tal y como queda de manifiesto en el valor del nivel crítico p.
Interpretar el resultado en
función del contexto de la investigación.
El curso realizado por el psicólogo ha
obtenido los resultados esperados:
- demostrando su utilidad para fomentar la asertividad en los directivos de su departamento.
Intervalo de confianza.
Podemos calcularlo mediante la Ecuación
Que aplicándola a nuestros datos:
Con lo que interpretaríamos, a un nivel
de confianza del 95% que:
- la media en asertividad es menor antes del curso (ambos límites son negativos y no contienen el valor cero plateado en la hipótesis nula),
Observándose un aumento después del curso:
- que oscila entre 1’107 y 7’893 puntos en la puntuación media del test.
Emplearemos este contraste de hipótesis
para comparar dos proporciones poblacionales cuyos valores se estiman a partir
de los datos observados en la misma muestra de sujetos, siendo la variable
dependiente dicotómica o dicotomizada.
Como se ha indicado anteriormente, la variable dependiente presenta dos
opciones mutuamente excluyentes como, por ejemplo: “Sí”, “No”; “A favor” o
“En contra”, “Aprobado”, “Suspenso”, etc., donde se trata de comparar la
proporción de éxitos en las dos condiciones que presenta la variable independiente en función de las
hipótesis establecidas.
También se indicó con anterioridad, que
una de las ventajas de trabajar con datos
dicotómicos consiste en que los supuestos no son tan estrictos como en el
caso de las variables continuas.
Tan sólo es preciso que los tamaños de las muestras sean lo
suficientemente grandes para poder asumir la normalidad de la distribución
muestral de las diferencias entre proporciones.
Generalmente se
empleará este contraste de hipótesis cuando se miden los datos de la muestra en
la variable dependiente en dos momentos temporales distintos, como por ejemplo
“antes” y “después” del tratamiento o “tratamiento A” vs. “tratamiento B”.
Estadístico Z.
El razonamiento para el contraste de
hipótesis sobre dos proporciones para muestras relacionadas es el mismo que el
visto en el caso de dos muestras independientes, y se basa en que la distribución
muestral de la diferencia de proporciones es una distribución normal cuando se
trabaja con muestras grandes, siendo el estadístico de contraste una puntuación
típica con la siguiente expresión general:
Para aplicar este estadístico con el fin
contrastar:
Primero se organizan los
datos en una tabla de doble entrada de 2x2, denominada Tabla de Contingencia:
Los respuestas de los N sujetos recogidos
en esta tabla de contingencia se reparten en las cuatro celdillas con a, b, c y
d observaciones.
En la muestra, la proporción de sujetos
con respuesta de “éxito” antes de introducir la variable independiente es un
estimador insesgado de la proporción poblacional y corresponde a:
De igual forma, la proporción de sujetos
con respuesta de “éxito” después de introducir la variable independiente, es:
La hipótesis nula a contrastar es que las
dos proporciones poblacionales (estimadas a partir de los datos de la muestra)
son iguales, es decir:
Si las dos proporciones poblacionales son
iguales, entonces, su diferencia a partir de sus estimadores muestrales es:
Si la hipótesis nula es cierta entonces las frecuencias de las celdillas b y c son iguales:
Se puede demostrar que el error típico de la
distribución muestral de la diferencia de dos proporciones:
Para muestras relacionadas, es:
Si las dos proporciones son iguales entonces:
El error típico de la distribución muestral
quedaría simplificada a:
Siendo el estadístico de contraste Z:
Finalmente:
A partir de esta expresión, para la aplicación del estadístico
Z solo se tiene en cuenta a los individuos que aportan información.
- que son aquellos que han obtenido resultados distintos bajo una u otra condición.
- aquellos cuya puntuación es diferente en las dos condiciones en las que medimos la variable dependiente o respuesta.
- solo utilizaremos los n sujetos de las casilla b y c (n=b+c).
Si el tamaño de esta muestra de sujetos
es suficientemente grande (n>25) podremos aplicar el estadístico Z o el
estadístico de McNemar que veremos más adelante.
Ejemplo 4.3. Un empresario, antes de introducir en el mercado un
determinado producto “X”, toma una muestra aleatoria de 500 sujetos de la
población a la que quiere dirigirse y les pregunta si comprarían o no dicho
producto. A continuación les muestra las posibles ventajas que aporta el
producto “X” y les vuelve a preguntar si lo comprarían. Antes de la
demostración de las ventajas del producto “X”, 400 personas declaran que no lo
comprarían, mientras que después de la demostración son 380 personas las que no
lo comprarían. Por otro lado 60 personas estarían dispuestas a comprar el
producto “X” tanto antes como después de la demostración. ¿Podemos afirmar al
nivel de confianza del 99% que, la demostración del producto “X” ha sido
eficaz?
Construimos la siguiente
tabla de contingencia con los datos proporcionados en el enunciado:
A continuación completamos fácilmente el
resto de la tabla.
Sujetos que comprarían “X” antes de la
demostración:
Sujetos que comprarían “X” después de la demostración:
Una vez deducidas las frecuencias
marginales:
La tabla de contingencia queda de la siguiente forma:
En este contraste sólo nos interesan
los sujetos que han cambiado de opinión tras la presentación de “X”
(casillas “b” y “c”).
- En general, aquellos sujetos cuya puntuación es diferente en los dos momentos en los que medimos la variable dependiente.
- si el número de cambios es el mismo en las dos direcciones (hipótesis nula)
- o si, por el contrario, la mayor parte de los sujetos que cambian de opinión lo hacen en una dirección determinada (hipótesis alternativa).
Los datos obtenidos, muestran que:
- 60 sujetos han cambiado de opinión en la dirección que pretendía el empresario (casilla c) puesto que declararon que no comprarían “X” antes de la demostración y sí después.
- tenemos 40 sujetos que han cambiado de opinión en la dirección contraria (casilla b).
Condiciones y supuestos.
Contamos con 100 observaciones
independientes y una variable dicotómica, donde definimos el éxito como: “No
antes, Sí después” y el fracaso como “Sí antes, No después”. En general
tendremos:
- Variable dependiente dicotómica o dicotomizada
- Muestra con “b+c” observaciones independientes, donde b+c
> 25.
Hipótesis.
La hipótesis nula especifica que la
proporción de éxitos es igual o menor que la de fracasos, y la alternativa que
la proporción de éxitos es superior a la de fracasos.
Estadístico de contraste y
su distribución muestral.
Aplicando el estadístico Z
Regla de decisión:
En un contraste unilateral izquierdo, con un nivel de confianza de 0,99,
el valor crítico es:
Como el estadístico de contaste
, es superior al valor crítico -2,33, no tenemos evidencia suficiente para rechazar la hipótesis nula que se
mantiene como provisionalmente verdadera.
Consultamos en las tablas de curva normal
el nivel crítico, que es: p=0,0228 que
al ser mayor que el nivel de significación (
),
no nos permite rechazar
con un nivel de confianza del 99%.
Interpretar el resultado en
el contexto de la investigación.
Los resultados obtenidos no superan el
nivel de confianza fijado de antemano, pero por otro lado, como se puede
apreciar al examinar el nivel crítico, sí
son significativos al nivel de confianza del 95%.
En cualquier caso:
- de un total de 400 personas que no comprarían el producto “X” inicialmente
- tan sólo 60 han cambiado de opinión en la dirección que pretendía el empresario
- y 40 personas han cambiado de opinión en la dirección contraria.
El empresario del ejemplo debería
considerar si es rentable la campaña publicitaria que ha diseñado, puesto que
en total, tan sólo se incrementa en 20 personas el número de posibles clientes
que ganaría tras la demostración del producto “X”.
Este contraste podríamos haberlo realizado
si consideramos que tenemos una única muestra de 100 observaciones, definiendo
el “éxito” como:
- “no antes” y “si después”, se pueden plantear las siguientes hipótesis:
Siendo el estadístico de contraste igual
a:
Estadístico de McNemar.
Prueba estadística muy utilizada en
Psicología es el test de McNemar, cuyo estadístico de contraste es:
Este estadístico es el cuadrado del
anterior se distribuye según Chi cuadrado con un grado de libertad.
Los supuestos y las hipótesis para
aplicar el test de McNemar son iguales a las tratadas para el estadístico Z:
El nivel crítico, calculado con un
programa informático es igual a p=0,0455 (mediante las tablas deduciríamos que
está comprendido entre):
- 0,025<p<0,05
El estadístico de contraste se encuentra entre
los valores 3,84 y 5,0239.
Podemos apreciar que el nivel crítico p
es mayor para Chi cuadrado que para Z, lo que sucederá siempre que el contraste
sea unilateral, siendo en este caso más difícil rechazar la hipótesis nula con
el test de McNemar.
- Si el contraste fuera bilateral el nivel crítico sería el mismo para ambos estadísticos.
En el ejemplo que hemos desarrollado, el
contraste es unilateral, lo que no plantearía ningún problema si utilizamos el
estadístico Z, pero si empleamos el estadístico ji-cuadrado
No obstante, el investigador puede
interpretar los datos, y por lo tanto la dirección de las diferencias,
fijándose en cuál de las dos casillas “b” o “c” presenta una frecuencia mayor.
La diferencia entre los estadísticos Z y
, consiste en que el estadístico es
insensible a la dirección del cambio producido. En nuestro ejemplo, el valor de
ambos estadísticos es:
Observamos que ji-cuadrado es siempre positivo, puede detectar que existe un cambio pero no detecta la dirección del cambio. Por ello con este estadístico no se puede plantear una hipótesis estadística unilateral.
No tiene sentido rechazar la
hipótesis nula si obtenemos un valor muy pequeño, lo que nos indicaría que el
número de sujetos que cambian de opinión en ambas direcciones son muy
parecidos.
De hecho, como podemos
apreciar en la Ecuación:
Ji cuadrado valdrá cero cuando
“b=c” que es precisamente lo que postula
la hipótesis nula.
Es decir,
al aplicar la prueba de McNemar siempre dejamos todo el nivel de significación
(α) en la parte derecha de la distribución.
En la
Figura 4.3 mostramos cuándo mantener o rechazar la hipótesis nula:
Establecer
regla de decisión en función del nivel de confianza.
Buscando en las
tablas el valor críticos al nivel de confianza del 99%, tenemos que:





























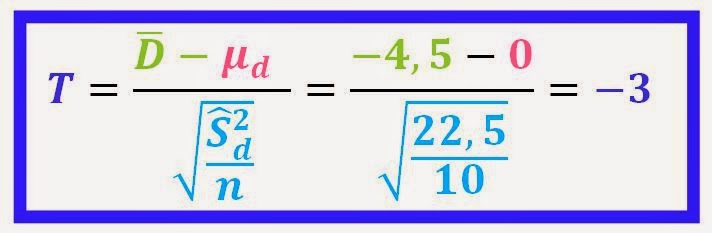












































Comentarios
Publicar un comentario